Ever wondered why slicing a cone gives an ellipse? It’s wonderfully clever!
Dandelin spheres, conic sections, and a view of genius in math.
Brought to you by you: http://3b1b.co/dandelin-thanks
Home page: https://www.3blue1brown.com
Thoughts on the recent change to be sponsor-free:
https://www.patreon.com/posts/going-sponsor-19586800
Video on Feynman’s lost lecture: https://youtu.be/xdIjYBtnvZU
I originally saw the proof of this video when I was reading Paul Lockhart’s “Measurement”, which I highly recommend to all math learners, young and old.
New shirts/mugs available: http://3b1b.co/store
The 3d animations in the video were done using Grapher, while 2d animations were done using https://github.com/3b1b/manim
If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then “add subtitles/cc”. I really appreciate those who do this, as it helps make the lessons accessible to more people.
Music by Vincent Rubinetti:
https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown
——————
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribe
Various social media stuffs:
Website: https://www.3blue1brown.com
Twitter: https://twitter.com/3blue1brown
Reddit: https://www.reddit.com/r/3blue1brown
Instagram: https://www.instagram.com/3blue1brown_animations/
Patreon: https://patreon.com/3blue1brown
Facebook: https://www.facebook.com/3blue1brown
source

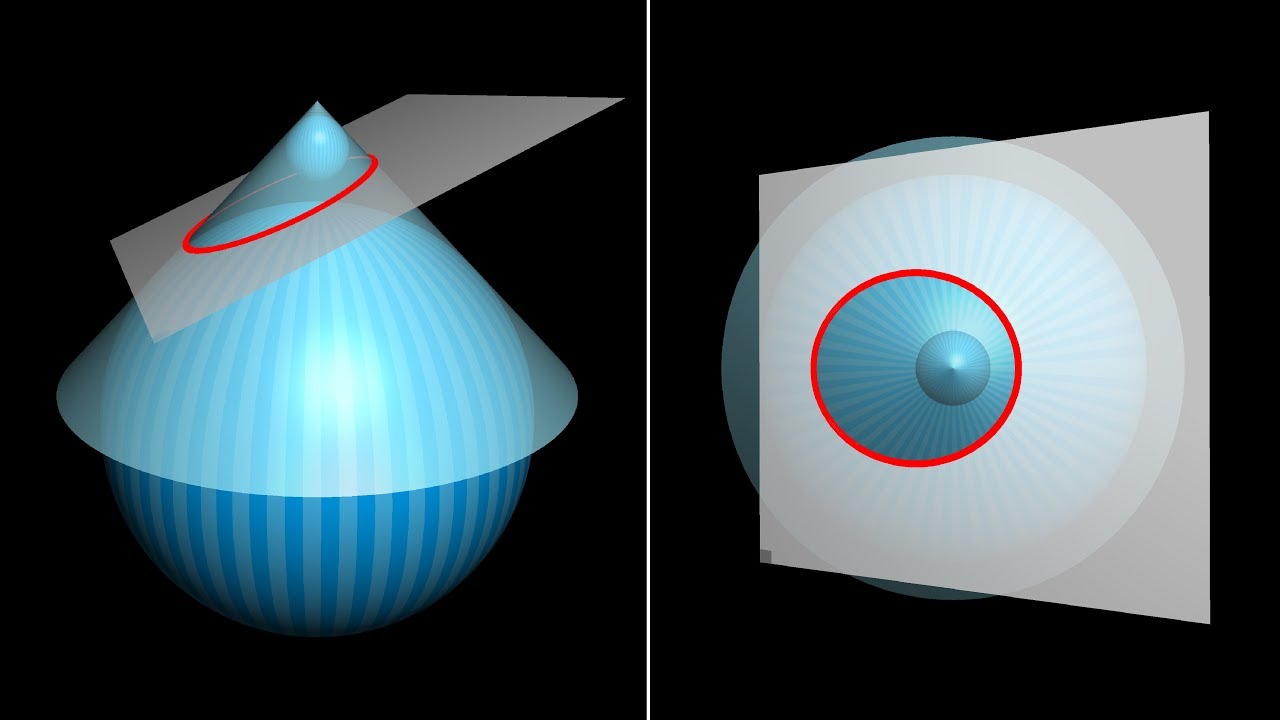
No, I didn't.
Oh. We’re talking about an oval. Not …
Ever wonder what an ellipse is?
Cause yeah, same.
Отдельное спасибо человеку, решившему, что перевести название и описание видео куда важнее субтитров. МОЛОДЕЦ ГЕНИЙ.
No, ive never wondered that.
Mainly assertions. As far as “proof” — you don’t demonstrate WHY it’s true.
3 words…oh my god!???
I can trace my life-long love of math to 9th grade when my algebra teacher, as an aside to the lesson, but with enthusiasm, demonstrated the equivalence of repeating decimals and fractions. It seems so simple now, but at the time the question had never occurred to me, so to see how simple it is was so delightfully surprising. It left me hungry for more.
Good luck explaining the proof without the 3d animation.
I was wrapping my head around why slicing a cone gives an ellipse for ages! Now, I finally know.
Grant, I love your videos, and you are doing good works making such informative and intuitive educational material, but it's pronounced as «fo-kai», not «fo-sai»
How do you produce your animations?
Also we should be able to draw smaller cones from the perimeter of the ellipse to the ball that is tangent at the focus and the line on the bigger cone right?
Me: Just going about my daily life.
3Blue1Brown: Ever wondered why slicing a cone gives an ellipse?
Me: I wonder why slicing a cone gives an ellipse.
Exactly one year ago
Please make a video on binomial and polinomical
Why did he think of fitting in two sphere and why not elipsoids instead??? I know that two tangent of a sphere meet at a point then they have similar length which doesn't happen to in case of elipsoid , but still how he got that idea how genius could people get??
9:18 bada boom bada BING
“It’s wonderfully clever”
Did you just double-space on me?
Beautiful proof!
OK so why does a circle viewed obliquely look like an ellipse? It's trivial to show that the projection of circle onto an oblique plane is an ellipse, but the bundle of rays forming the image of the oblique circle to your eye does not form a neat round cone but a squashed cone with a perfectly elliptical cross section why?
He said foh-sai 🙁
Can you show were is it's diretrix ???
Well if you cut a cone in the horizontal direction, its a circle…
is it just me or the thumbnail looks like a breast a 90° ? for me that's the real genius of math ! 😀
How much is the Eccentricity of Earth?
I would choose the fibonacci sequence, or the golden ratio.
Great Immanuel Kant reference at the end
One of my favorite channels.
Actual Perfection.
Just clicked the video for the nipple in the thumbnail.
Tambien se podria pensar que si la definicion de una elipse viene con la suma de las distancias de los focos, esto, en el caso de las chinchetas y su exentricidad se define como la distancia de estos, en el caso del cono la exentricidad se definiria en relacion con la inclinacion del plano, entre mas inclinado este el plano, mas exentricidad se tendria.
mr pi, you're late for klass, you're suposed to be here at 0:56 and 3:14
Basically saw a b00b and came here
"non-math enthusiast"
triggered
8:32 is that sputnik 1
I agree, demonstrations often relies on other mind technics applied on more or less related topics . The more you are immersed into, the more likely you can have the same state of mind. It's a kind of mental technology, we inherited a huge accumulation of very small increments, and you need to apply known technics to other field in order to "create". I would be very interested in an exhaustive list of all types of demonstrations known and the way they are connected.
No. I haven't.
(Opens a new video)